Hay muchos temas que poner y no sé por donde empezar, ¡demonios!
Vale, a ver que sale.
Antes de comenzar, traten de recordar mis abreviaciones, asi no tengo que alargar tanto esto, por ejemplo Pm: punto medio, m: pendiente, etc, más adelante lo verán.
Lección II: Nociones de Geometría Analítica
Pondré principalmente las formulas que se ocupan, de momento puede no haber una explicación detallada sobre su aplicación, en el siguiente artículo haré un ejercicio aplicando y explicando las formulas.
- Formula de la distancia entre dos puntos:
d= √ (x1 - x2)² + (y1 - y2)²
Donde:
(x1, y1) ---> son los valores del Punto P1
(x2, y2) ---> son los valores del Punto P2
- Formula para hallar el punto medio
Pm(x)= x1 + x2/ 2
Pm(y)= y1 + y2/2
(Todo dividido entre dos)
Donde:
(x1, y1) ---> son los valores del Punto P1
(x2, y2) ---> son los valores del Punto P2
Los valores que obtengamos, son las coordenadas del punto medio, teniendo de coordenadas:
Punto medio ( Pm(x), Pm(y) )
- Formula de la pendiente
*Si conocemos el ángulo de inclinación de una recta dada
*Si conocemos el valor de dos puntos
Para el primer caso, la formula es la siguiente:
m= tg θ
Donde:m --> pendiente
tg --> tangente
θ --> valor del ángulo
Para el segundo caso, tenemos que:
m= y1 - y2/ x1 - x2
Donde:
m --> pendiente
(x1, y1) ---> son los valores del Punto P1
(x2, y2) ---> son los valores del Punto P2
Cabe mencionar que, cuando dos rectas son paraleas entre si, sus pendientes son iguales; y cuando dos rectas son perpendiculares, sus pendientes son reciprocas y de signo contrario, y el producto de ellas es igual a "-1"
- Ecuación de la recta de la forma punto-pendiente
y - y1= m ( x - x1)
Donde:
(x1, y1) --> son los valores del punto que tenemos o seleccionamos, segun el caso.
m --> valor de la pendiente que ya tenemos o que hallamos con dos puntos (ver formula de la "m")
"x" y "y" son términos que pertenecen a nuestra futura ecuación.
En la formula SUSTITUIREMOS VALORES SOLO para el punto y la pendiente.
- Ecuación de la recta de la forma simétrica
x / a + y / b = 1
Donde:
a --> es la intersección con el eje x
b --> la intersección con el eje y
Tienen un coordenada en cero "a" y "b" porque solo nos interesa donde cortan con los ejes, entonces tenemos que:
Las coordenadas para el punto de corte en el eje x son: P1 (a, 0)
Las coordenadas para el punto de corte en el eje y son: P2 (0, b)
Simplemente es pasar una ecuacion a esta forma.
- Ejemplo
Sea la ecuacion
2x + 3y + 6= 0
Primero pasamos el termino independiente, es decir el que no posee literal, el "6", al otro lado de igual.
2x + 3y= -6
Se vuelve negativo el "6", porque los términos que pasan al otro lado de igual deben cruzar con la operación contraria, la resta es contraria a la suma, solo para aclarar.
Ahora lo que haremos será dividir toda la ecuación entre el término independiente, con todo y signo en el caso de los negativos, ya que la ecuación debe ser igualada a "1", entonces...
2x/-6 + 3y/-6= -6/-6
Simplificamos...
x/-3 + y/-2 =1 [esta es nuestra ecuación]
Y nuestras coordenadas de los puntos de intersección son:
P1 (-3, 0)
P2 (0, -2)
Por cierto que los coeficientes de "x" y "y" tienen que valer 1.
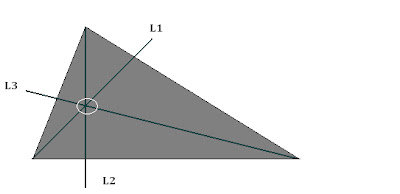
- Lineas, ó rectas, en un tríangulo
Entre las lineas o rectas que podemos encontrar en un triángulo están:
*Mediana
Es la linea recta que va de uno de los vértices del triángulo al punto medio del lado opuesto, el punto de intersección de las medianas se llama, Baricentro.
*Mediatriz
Linea perpendicular al punto medio de un segmento, el punto de intersección de las mediatrices se llama, Circuncentro.
*Altura
Linea que va de uno de los vértices del triangulo al lado opuesto siendo perpendicular, el punto de intersección entre las alturas se llama, Ortocentro.
Resumen de formulas. [Editando]





No hay comentarios:
Publicar un comentario